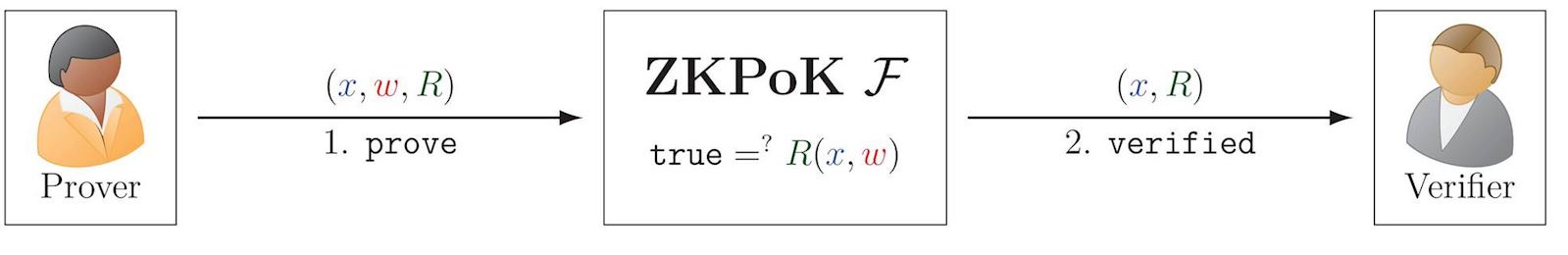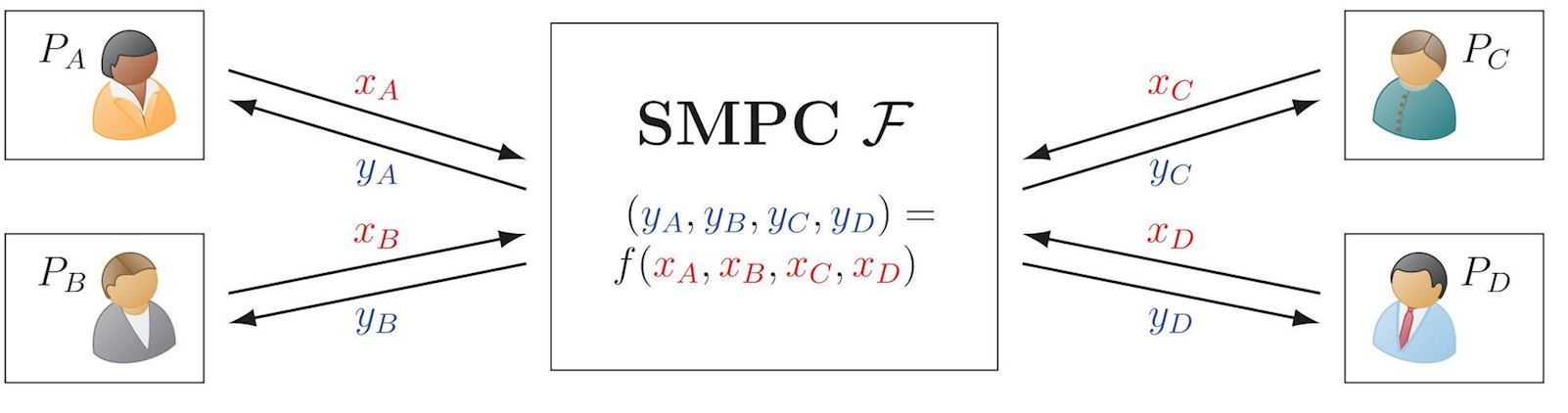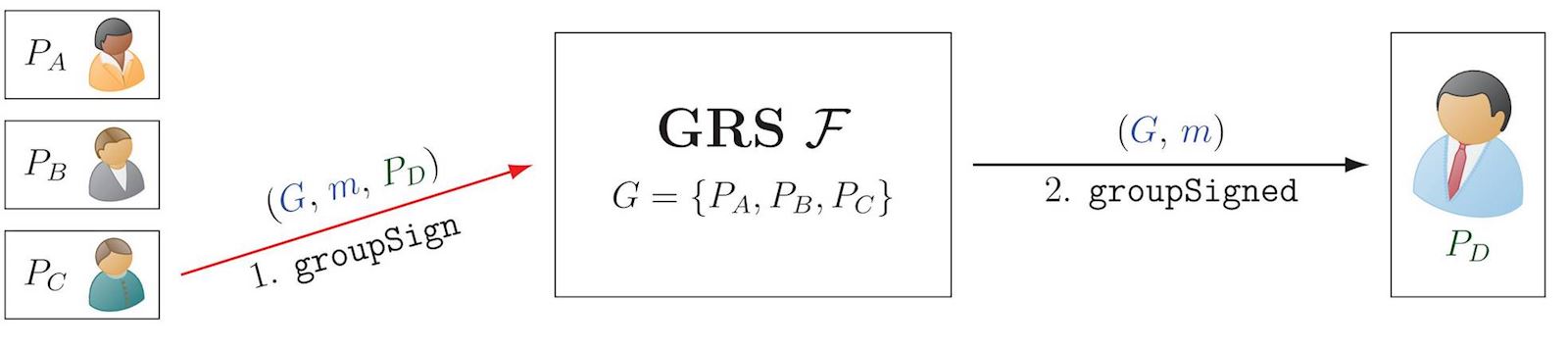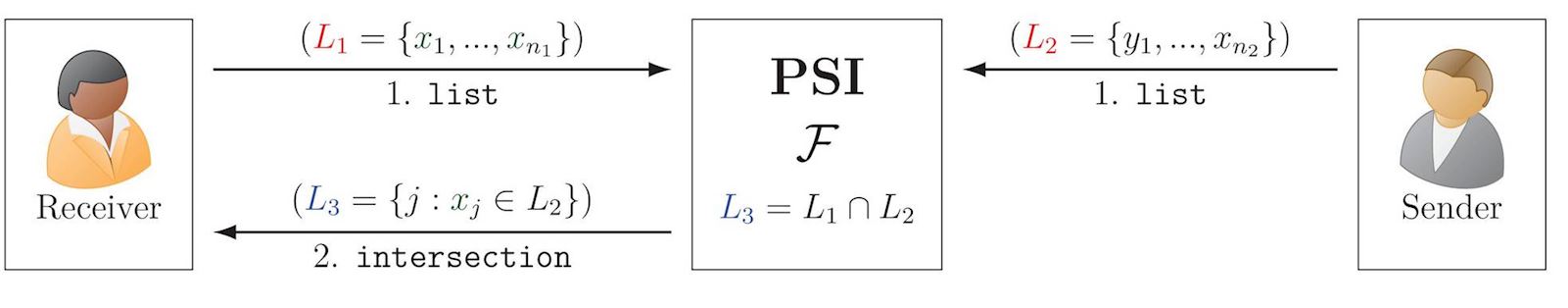PEC tools
PEC tools include a variety of cryptographic primitives, protocols and techniques useful for enabling privacy. This page uses simplified illustrations of "ideal functionalities" to convey a brief intuition about some representative PEC tools. It should be noted that real protocols for these PEC tools use cryptographic techniques in place of the trusted party (\(\mathcal{F}\)) represented in the figures.
Zero Knowledge Proof of Knowledge (ZKPoK)
A ZKPoK allows a prover to prove knowledge of a secret \(\color{red}w\) (also called witness), without disclosing it to the verifier. The secret is related to a public statement \(\color{blue}x\) and relation \(\color{darkgreen}R\). For example, this can apply to the knowledge of a secret private key corresponding to a public key. More formally, Alice can prove knowledge of \({\color{red}w}\) such that \({\tt true} =^? {\color{darkgreen}R}({\color{blue}x},{\color{red}w})\), where \(\color{blue}x\) is a public statement and \(\color{darkgreen}R\) is a relation.
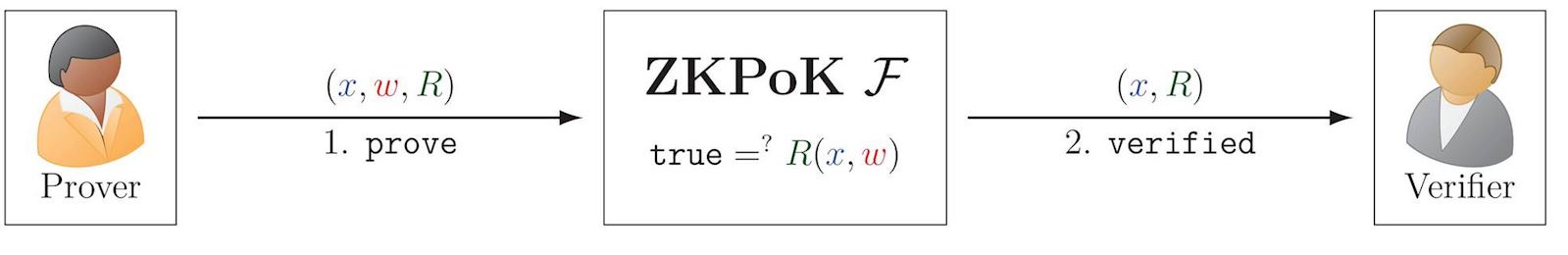
Secure Multiparty Computation (SMPC or MPC)
SMPC (more recently popularized as MPC) allows multiple distrustful parties to securely compute a function over their private inputs. This ensures privacy of the inputs and outputs, apart what each party can determine from their own input and output. MPC has many special cases and models of interest. For example, the simplified illustration below ignores aspects of fairness and abort. Of special interest is the assurance of security when some of the parties have been corrupted.
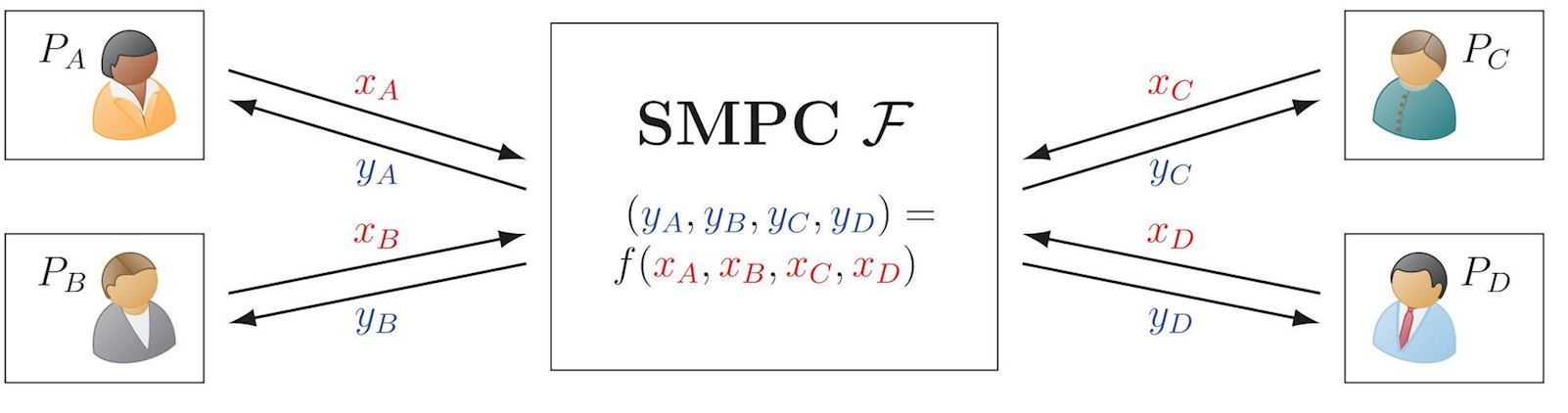
Fully Homomorphic Encryption (FHE)
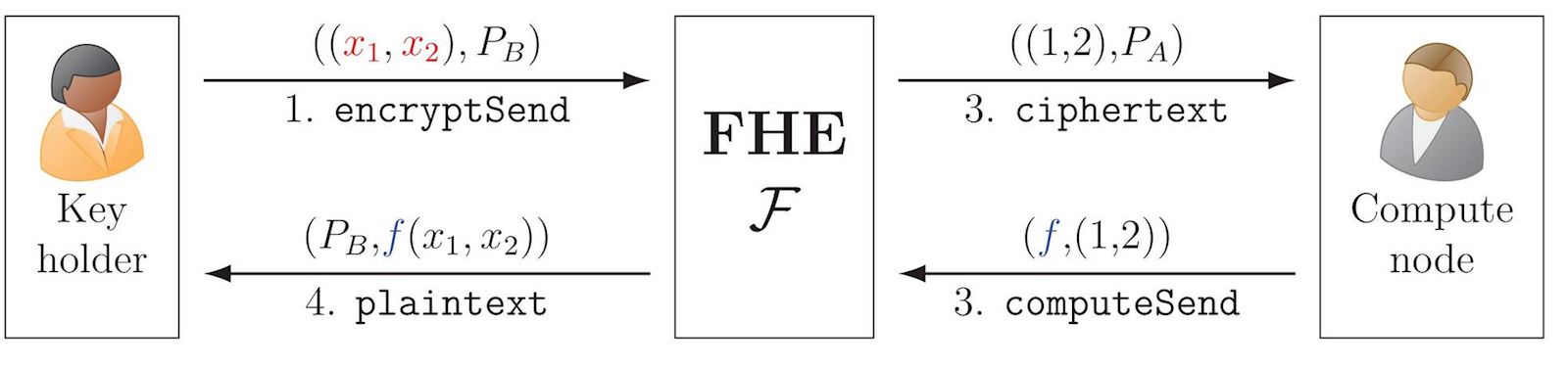
A homomorphic encryption scheme is a special type of encryption scheme that enables computing a function \(\color{blue}f\) over encrypted data, such that a later decryption outputs the function applied over the data. FHE enables this property for any computable function. This can be achieved both in the public-key setting and in the symmetric-key setting.
Group and Ring Signatures (GRS)
A group or a ring signature (here jointly denoted as GRS, though having relevant distinctions), allow a party to sign a message m on behalf of a group \(\color{blue}G\) of possible signatories. The signature can be verified as having been produced by a member of the group, without revealing who.
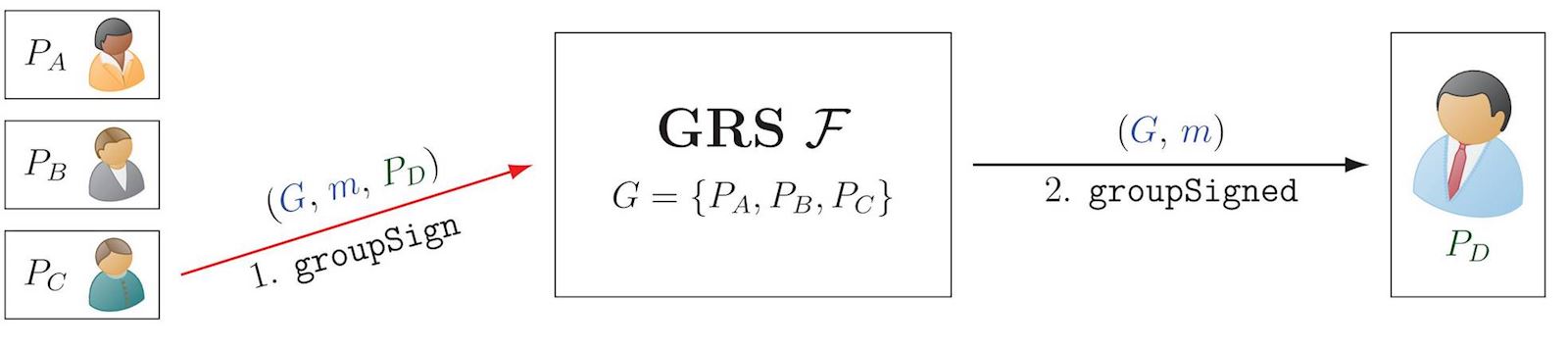
Private Set Intersection (PSI)
PSI allows two parties to compute the intersection of their sets, without disclosing the non-intersecting elements. If Alice has set \(\tt \{\red{p},{\color{blue}r},\red{i},\red{v},\red{a},{\color{blue}t},\red{e}\}\) and Bob has \(\tt\{\red{s},{\color{blue}e},\red{c},{\color{blue}r},{\color{blue}t}\}\), then Alice gets \(\tt\{{\color{blue}r},{\color{blue}t},{\color{blue}e}\}\). Interesting generalizations exist for PSI between multiple parties.
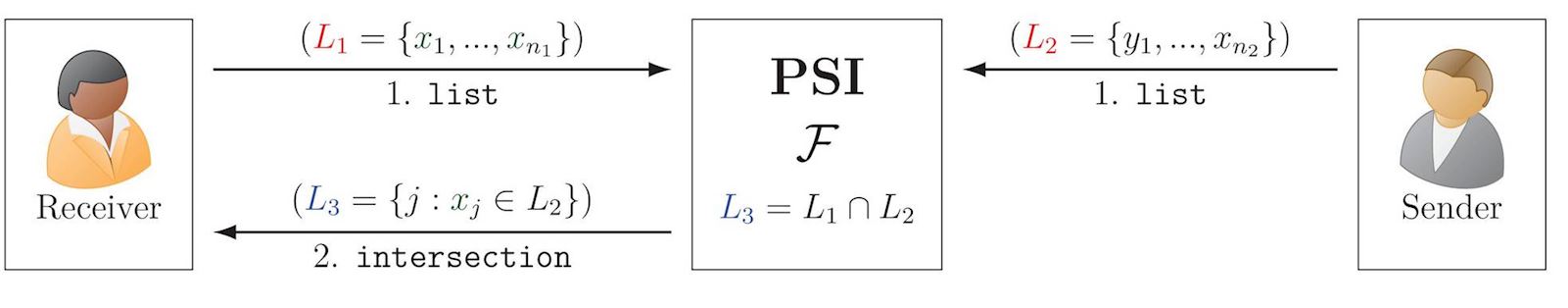
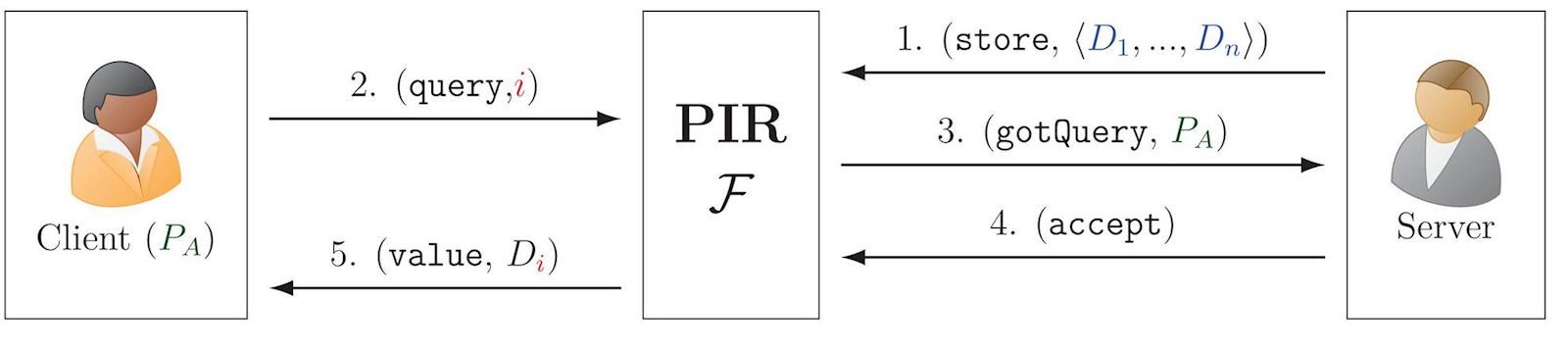
Private Information Retrieval (PIR)
PIR allows a client to retrieve an indexed value from a database held by a server, without the server learning what the query was. In the illustration, \(\color{blue}D\) is a key-value dictionary, such that \(D_{\red{i}}\) is the value associated with the key (aka label) \(\red{i}\).
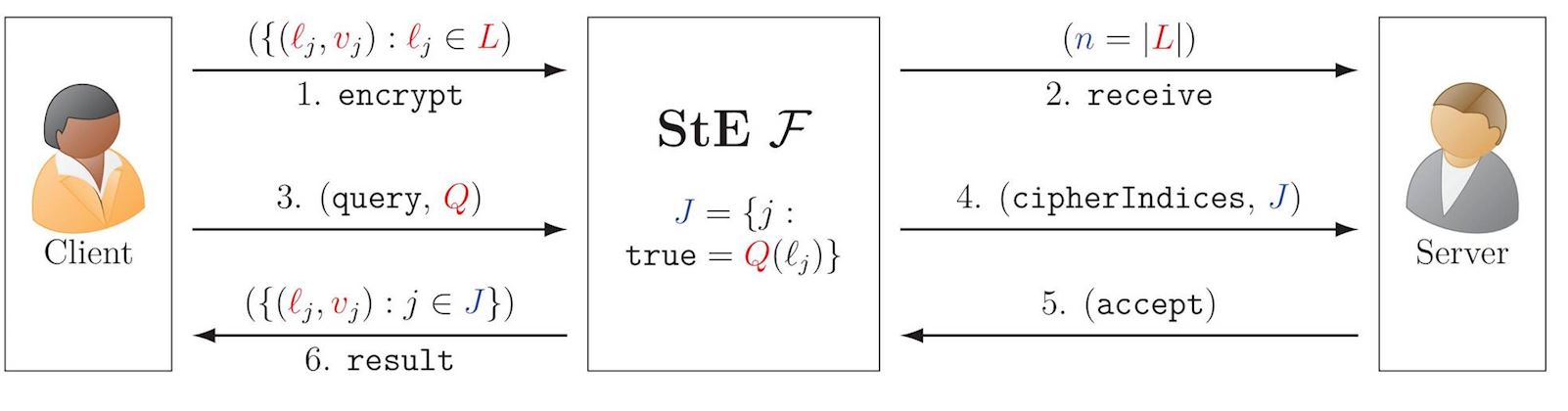
Structured Encryption (StE)
StE allows privately querying encrypted data structures. For example, a query (\(\red{Q}\)) for a dictionary — list of label-value pairs \((\red{\ell},\red{v})\) — specifies a label \(\red{\ell}_{\color{blue}j}\), to get as answer its corresponding value \(\red{v}_{\color{blue}j}\).
There are more PEC tools than those described here, ranging from multi-party protocols to lower-level building blocks. Some examples: functional encryption (FnE), which includes the special cases of attribute-based encryption (ABE) and identity based encryption (IBE); oblivious random-access memory (ORAM); commitment schemes, oblivious transfer (OT), and garbled circuits.
 An unofficial archive of your favorite United States government website
An unofficial archive of your favorite United States government website